Тема 1.5. Середні величини та показники варіації.

1. Середні величини в статистиці, їх значення. 
2. Середня арифметична. 
3. Середня гармонічна. 
4. Показники варіації, їх роль і значення. Види показників варіації, порядок їх розрахунку.

І. Середні величини в статистиці, їх значення.

Серед узагальнених показників, які застосовують для характеристики суспільних явищ і виявлення закономірностей їхнього розвитку, велике значення мають середні величини. 
Середня величина в статистиці — це абстрактна, узагальнююча величина, що характеризує типовий рівень варіаційної ознаки в розрахунку на одиницю однорідної сукупності. 
Вивчаючи суспільні явища з метою виявлення характерних закономірних рис у конкретних умовах місця й часу, статистика широко використовує середні величини. 
Середня через взаємне погашення індивідуальних значень дає змогу виявити загальну тенденцію розвитку. Тому тлумачення суті середніх виходять з положень закону великих чисел і його значення для середніх. Закон великих чисел створює умови, щоб у середній величині проявлявся типовий рівень варіаційної ознаки. 
Вимоги стосовно середніх: 
1) Визначення середньої на підставі масових даних. Індивідуальні значення досліджуваної ознаки в окремих одиниць сукупності мають бути різними. В разі узагальнення масових фактів випадкової відхилення індивідуальних величин від загальної тенденції взаємно погашаються в середній величині. Ця вимога в статистиці пов'язує середні величини із законом великих чисел. 
2) Якісна однорідність, одноманітність сукупності, для якої визначають середню. Це означає, що не можна застосувати середні до таких сукупностей, окремі частини яких підлягають різним законам розвитку відносно осереднюваної ознаки. 
У статистичній практиці використовують декілька видів середніх: 
- середня арифметична; 
- середня гармонічна; 
- середня квадратична; 
- середня геометрична. 
Кожна із зазначених середніх може набувати дві форми: просту й зважену. 
Якщо середня обчислюється за первинними (не згрупованими) даними, застосовується проста форма, якщо за вторинними (згрупованими) — зважена. 
Використання кожного виду середніх залежить від двох обставин: 
• по-перше, від характеру індивідуальних значень ознаки; 
• по-друге, від характеру алгебраїчного зв'язку між індивідуальними значеннями ознаки та її загальним обсягом. 
У статистиці для обчислення середніх постає питання вибору виду середньої у кожному конкретному випадку дослідження.

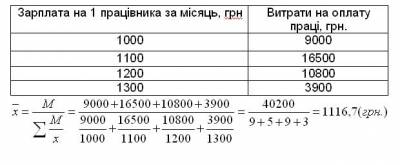
II. Середня арифметична.

Середня арифметична — одна з найбільш поширених видів середньої, застосовується у тих випадках, коли обсяг варіюючої ознаки для всієї сукупності є сумою індивідуальних значень її окремих елементів. 
Середня арифметична використовується для осереднення прямих значень ознаки шляхом їх підсумування. 
Логічна формула має вигляд: 
 
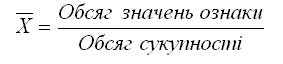
Якщо дані не згруповані, використовується середня арифметична проста. 
 
Приклад: Статутний фонд акціонерної компанії сформований 6 засновниками: розмір внеску кожного з них становить, тис.грн: 60, 100, 120, 90, 70, 40. 
Середній внесок одного засновника: 
 
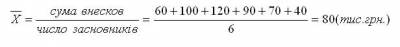
Якщо дані згруповані, то використовують середньозважену арифметичну: 
 
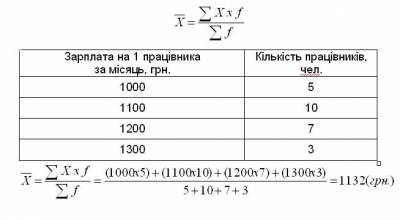
Властивості середньої арифметичної.

1) Алгебраїчна сума відхилень всіх варіант від середньої дорівнює нулю: 
 
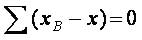
2) Якщо кожну варіанту збільшити або зменшити на будь-яку постійну величину, то і середня зміниться на ту же величину: 
 
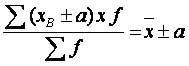
3) Якщо кожну варіанту розділити чи помножити на будь-яке число, то і середня зменшиться або збільшиться в стільки же разів: 
 
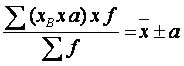
4) Якщо частоти всіх варіант збільшити або зменшити в одне й теж саме число разів, то середня при цьому не зміниться: 
 
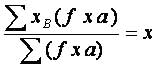
5) Сума квадратів відхилень варіант від середньої менша на будь-яку іншу величину: 
 
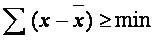
III. Середня гармонійна.

Середня гармонійна застосовується у тих випадках, коли нам відомі не самі вартості, а їхні обернені числа. 
Середня гармонійна використовується для осереднення індивідуальних значень ознаки шляхом їх підсумування. 
Для не згрупованих даних - це середня гармонійна проста: 
 
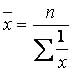
Якщо дані згруповані, то використовують середню гармонійну зважену: 
 
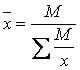
де М — обсяг значень ознаки, тобто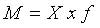  
Середню гармонійну зважену доцільно використовувати, коли відсутня інформація про значення знаменника логічної формули, тобто відсутні ваги. 
Середню гармонійну використовують тоді, коли вагою слугують не одиниці сукупності (носії ознаки), а добуток цих одиниць на значення ознаки, 
 
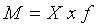
З цього правила випливає: середня гармонійна в статистиці — це перетворена середня арифметична, яку застосовують у разі, коли чисельність сукупності невідома, а варіанти зважуються обсягом ознаки. 
 
ІV. Показники варіації, їх роль і значення. Види показників варіації.

Середні величини як узагальнені показники характеризують сукупність за варіаційною ознакою, вказують на їх типовий рівень у розрахунку на одиницю однорідної сукупності. 
Проте середня величина не пояснює, як групуються навколо неї окремі значення; чи лежать вони поблизу, чи, навпаки, істотно відхиляються від середньої. 
Коливність окремих значень варіантів характеризують показники варіації. 
Термін «варіація» походить від латинського "Vагіаtiо" — зміна, коливність, різниця. У статистиці під варіацією розуміють кількісні зміни ознаки в межах однорідної сукупності. 
У статистиці розроблено цілу систему показників варіації, які використовують для всебічної характеристики рядів розподілу і їх можна виражати як в абсолютних, так і відносних величинах. 
У системі показників варіації найпростішим є показник розмаху варіації, який визначають як різницю між найбільшим і найменьшим значенням варіантів. 
 
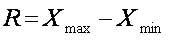
В інтервальних рядах розподілу розмах варіації визначають як різницю між верхньою межею останнього та нижньою межею першого або як різницю між серединами інтервалів. 
Перевагою показника розмаху варіації є простота його розрахунку. Однак він не може повною мірою охарактеризувати варіацію ознаки, оскільки не враховує всіх значень ознаки, проміжних між макси¬мальним та мінімальним значеннями. Не враховує він і частот. Особливість показника розмаху варіації полягає у тому, що він залежить лише від двох крайніх значень ознаки, які можуть виявитися не достатньо типовими. 
Розмах варіації відображає інколи випадкове, а не типове для даного ряду коливання. Зазначені недоліки розмаху варіації звужують область його практичного застосування. В основному він використовується для попередньої оцінки варіації. Тому необхідні інші показники варіації, які ґрунтуються на всіх значеннях ознаки в даній сукупності. 
Більш досконалим показником вимірювання варіації є середнє лінійне та середнє квадратичне відхилення, які усувають зазначені недоліки розмаху варіації. 
Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень відхилень окремих варіант від середньої арифметичної. 
 
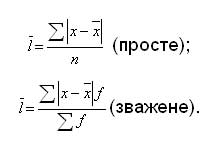
Прямі дужки означають, що абсолютні значення відхилень беруться по модулю, тобто підсумовування виконується без врахування знаків (плюс або мінус). Така умовність пояснюється тим, що оскільки сума відхилень індивідуальних значень ознаки від середньої в першому ступені дорівнює нулю (нульова властивість середньої арифметичної),то для одержання суми всіх відхилень, відмінної від нуля, кожне відхилення слід брати як додатну величину. 
Показник середнього лінійного відхилення більш обґрунтований порів¬няно з розмахом варіації. Він не залежить від випадкових коливань крайніх значень, оскільки спирається на всі значення ознаки, враховує всю суму відхилень індивідуальних варіантів від середньої арифметичної та частоти. 
Однак і цей показник варіації має суттєві недоліки. В ньому не враховуються знаки (спрямованість) відхилень. Довільне відки¬дання алгебраїчних знаків відхилень призводить до того, що математичні властивості цього показника є далеко не елементарними, а це значно усклад¬нює використання середнього лінійного відхилення при розв'язанні задач, пов'язаних з імовірнісними розрахунками. Тому середнє лінійне відхилення використовується рідко. 
Ступінь варіації об'єктивніше відображує показник середнього квадрата відхилення (дисперсія). Його обчислюють як середню арифметичну із суми квадратів відхилень окремих варіантів від їхньої середньої: 
 
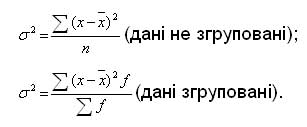
Корінь квадратичний із середнього квадрата відхилень варіантів від їхньої середньої називають середнім квадратичним відхиленням. 
Середнє квадратичне відхилення буває просте і зважене. 
 
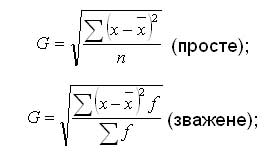
Середнє квадратичне відхилення є абсолютним виміром варіації, це означає, що порівнювати їх у варіаційних рядах різних явищ не можна. 
Змістовне значення середнього квадратичного відхилення таке ж саме, як і середнього лінійного відхилення. Воно показує, на скільки в середньому відхиляються індивідуальні значення варіант від їх середнього значення. 
Середнє квадратичне відхилення є критерієм надійності середньої. Чим воно менше, тим краще середня арифметична відображає всю досліджува¬ну сукупність. Перевага середнього квадратичного відхилення порівняно з середнім лінійним відхиленням полягає у тому, що при розрахунку ніякого умовного припущення про підсумовування відхилень без врахування знаків не допускається, оскільки всі відхилення підносяться до квадрату. 
Середнє квадратичне відхилення - це стандартне відхилення. Воно як розмах варіації й середнє лінійне відхилення є величиною іменованою та виражається в тих самих одиницях вимірювання, що і ва¬ріанти досліджуваної ознаки і середня величина (ц, кг, грн., м, ц/га і т.д.). 
Дисперсія і середнє квадратичне відхилення широко застосовуються на практиці. Вони входять в більшість теорем, які є фундаментом математичної статистики. Крім того, дисперсія може бути розкладена на складові елементи, які дають змогу оцінити вплив різних фак¬торів, що зумовлюють варіацію досліджуваної ознаки. 
При порівнюванні ступеня варіації однієї і тієї ж ознаки в різних сукупностях використовують коефіцієнт варіації. 
Розраховується як відношення абсолютних характеристик варіації до середньої і виражається відсотками.